Martin Spasov
Deriving Camera Transform
There are numerous articles on the internet that walk you through the creation of a view/camera transform, and this will be no different, though, I will try to add some additional context that might be useful. I’ll link some articles that have helped me better understand the subject at the end.
If you find any errors let me know and I’ll correct them!
Change of basis
The first topic I want to talk about is change of basis. A basis is a set of vectors that allows us to express any vector in a given vector space. For example (1,0,0), (0,1,0),(0,0,1) is one such set that describes vectors in R3 and is called the natural basis. If we negate one of those 3 vectors we get a new basis ((-1,0,0), (0,1,0),(0,0,1) ) and so on. As long as the set of vectors are linearly independent and they span the vector space they are a valid basis.
Change of basis is the process that allows us to take a vector v that is in basis A and express it in basis B. Let’s look at an example.
A - basis for R3 - (2,1,0), (0,0,1), (1,-2,0)
B - basis for R3 - (1,1,1), (1,-1,0), (1,1,-2)
v - (5,2,4) - vector expressed in A. The full expression is thus
v = 5 * (2,1,0) + 2 * (0,0,1) + 4 * (1,-2,0)
The goal is to figure out what v will look like when expressed in terms of B.
Approach #1
The first thing we want to do is to express the basis vectors of A in terms of B. To do that we need to create 3 systems of equations (one for each basis vector in A) using augmented matrices. The coefficient part of the matrix will correspond to the basis vectors of B and the constant part will correspond to a basis vector of A . Solving the systems of equations yields the basis vectors of A expressed in B. In theory we can do that for all vectors of A but there is a faster way (matrix multiplication is faster than solving a linear system).
----B--- -A-
1 1 1 | 2 1
1 -1 1 | 1 = 0.5
1 0 -2 | 0 0.5
----B--- -A-
1 1 1 | 0 0.333
1 -1 1 | 0 = 0
1 0 -2 | 1 -0.333
----B--- -A-
1 1 1 | 1 -0.333
1 -1 1 | -2 = 1.5
1 0 -2 | 0 -0.1666
Next thing we need to do is build a matrix T that will have the transformed vectors as its columns
1 0.333 -0.333
0.5 0 1.5
0.5 -0.333 -0.166
Now we can multiply v by T and the result will be v expressed in B
1 0.333 -0.333 5 4.33
0.5 0 1.5 * 2 = 8.5
0.5 -0.333 -0.166 4 1.16
The vector v expressed in B is (4.33, 8.5, 1.16).
The above matrix works for all vectors in A not just for v. Any vector that we have in A multiplied by T will give us the same vector expressed in B. We have created a transformation matrix A -> B
What if we want to perform the opposite operation ? What if we have a vector in B and we want to express it in A ? We have two options:
- repeat the same process as above but use the vectors of
Aas a coefficient matrix and the vectors ofBas constant vectors. - invert the transformation that we already have -
inverse(T)will give usB -> Atransform.
Approach #2
This is kind of a shortcut approach but basically we are going to use the formula below
TA->B = TE->B* TA->E
Where E is the natural basis - (1,0,0), (0,1,0), (0,0,1). All this formula does is that it first transforms the vector from A to E and then from E to B in order to achieve the same result as with the first approach.
Lets start with the first transform TA->E. If we follow the same steps as the first approach we get
----E--- -A-
1 0 0 | 2 2
0 1 0 | 1 = 1
0 0 1 | 0 0
----E--- -A-
1 0 0 | 0 0
0 1 0 | 0 = 0
0 0 1 | 1 1
----E--- -A-
1 0 0 | 1 1
0 1 0 | -2 = -2
0 0 1 | 0 0
As you can see, TA->E is simply the basis vectors of A
2 0 1
1 0 -2
0 1 0
Now for the second transformation we have
TE->B = inverse(TB->E)
1 1 1 0.333 0.333 0.333
inverse( 1 -1 1 ) = 0.5 -0.5 0
1 0 -2 0.166 0.166 -0.333
Finally, the full transform is
----- E->B --------- - A->E -
0.333 0.333 0.333 2 0 1 1 0.333 -0.333
0.5 -0.5 0 * 1 0 -2 = 0.5 0 1.5
0.166 0.166 -0.333 0 1 0 0.5 -0.333 -0.166
As you can see this approach results in the same change of basis matrix.
Here is an article that goes over change of basis in a bit more detail.
Active and Passive transformations
The second topic I wanna talk about are active and passive transformations. Basically, there are two ways we can interpret a transformation matrix. Lets take for example the below matrix
0 -1
1 0
Active Transformation interpretation
The above transformation rotates a vector v in coordinate system (basis) A and produces a vector v' that is in the same coordinate system. Active transformations do not change the basis of the vectors.
Example:
0 -1 * 2 = -2
1 0 2 2
Both (2, 2) and (-2, 2) are in the same coordinate system.
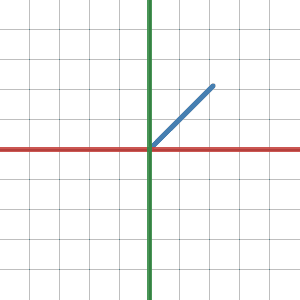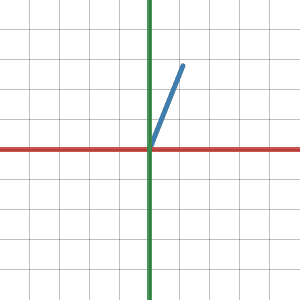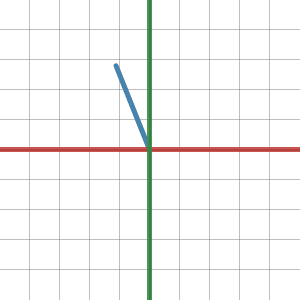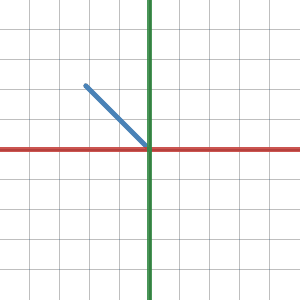
Passive Transformation interpretation
Passive transformations on the other hand change the coordinate system of the vector (aka change of basis). They do not move the vector, they tell us how the same vector is described with respect to a different basis. The above matrix thus represents a transformation TB->E where B is a coordinate system with the basis vectors (0,1), (-1,0) and E is the natural basis.
Example:
0 -1 * 2 = -2
1 0 2 2
(2,2) - vector described with respect to basis B
(-2,2) - same vector but described with respect to the natural basis
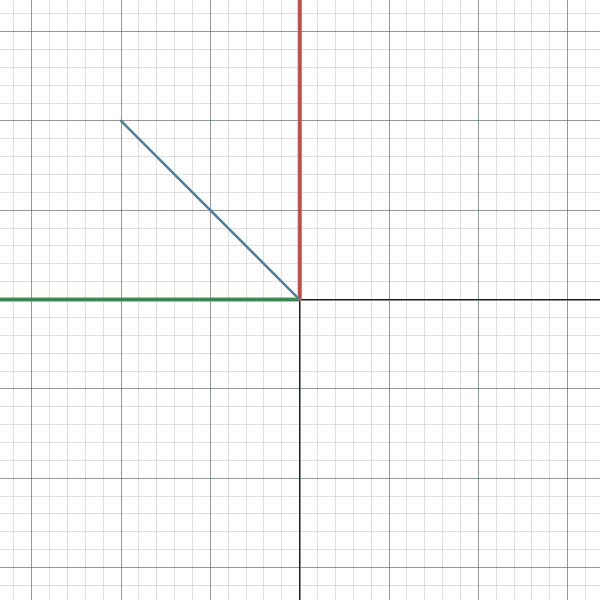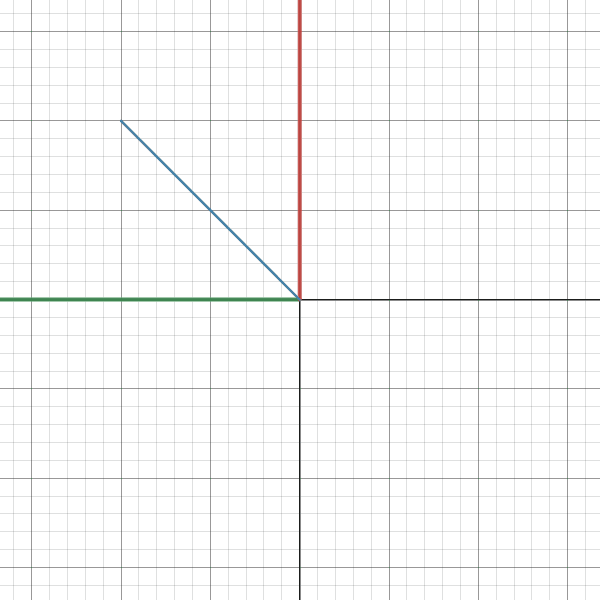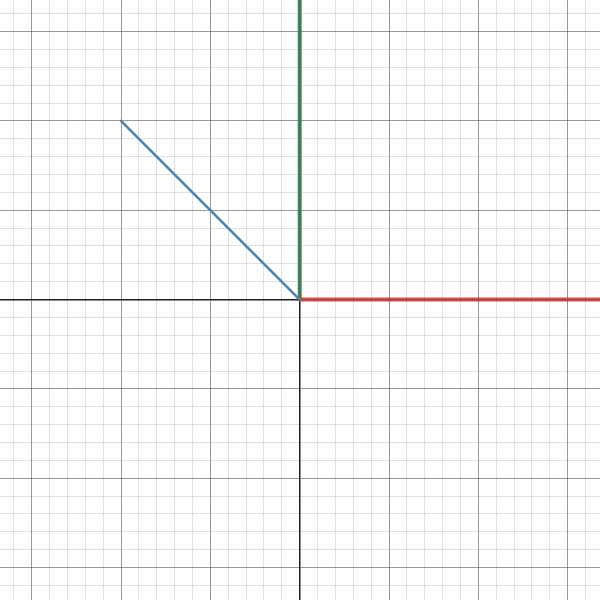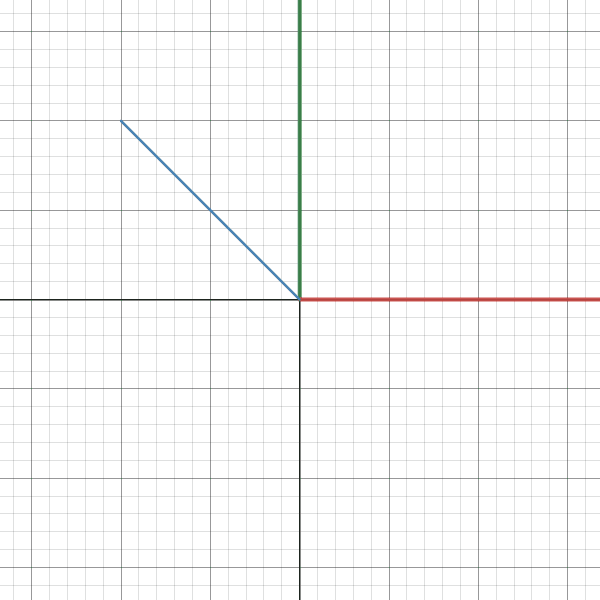
The first part of the gif shows the vector with respect to basis B and the second part shows the same vector with respect to basis E. As you can see the axes rotate (x - red, y - green).
Camera Transform aka the View Matrix
With the previous two sections covered we are now ready to talk about the camera transform. This transform is nothing more than just a change of basis (from world coordinate system to camera coordinate system). Let’s ignore the translation for now and assume that the camera is at the center already. We’ll come back to that later.
Camera basis vectors
Depending on the type of camera there are different ways we can derive the basis vectors
– LookAt Camera –
In this case the camera looks at a target (World of Warcraft, New World etc). Getting the basis vectors is pretty straight forward.
forward = normalize(cameraPosition - targetPosition)
right = normalize(cross((0,1,0), forward))
up = normalize(cross(forward, right))
The order of the vectors in the cross product operation depends on the right hand rule. Also keep in mind that the forward vector points towards the camera.
– First Person Camera –
We are going to use Euler angles for this type of camera. We will use only the pitch and yaw angles (no roll). The pitch will represent a rotation about the x axis and yaw will be a rotation about the y axis (see the image below for reference). We want the camera forward vector to point in the negative Z axis (OpenGL convention) so we will use (0,0,-1) as our initial direction.

cos(yaw) 0 sin(yaw) 1 0 0 0
forward = 0 1 0 * 0 cos(pitch) -sin(pitch) * 0
-sin(yaw) 0 cos(yaw) 0 sin(pitch) cos(pitch) -1
cos(yaw) sin(yaw)sin(pitch) sin(yaw)cos(pitch) 0
forward = 0 cos(pitch) -sin(pitch) * 0
-sin(yaw) cos(yaw)sin(pitch) cos(yaw)cos(pitch) -1
-sin(yaw)cos(pitch)
forward = sin(pitch)
-cos(yaw)cos(pitch)
forward = normalize(forward)
forward = -forward
right = normalize(cross((0,1,0), forward))
up = normalize(cross(forward, right))
Now that we have the basis vectors (from either the lookat or fps camera) we can define a transformation TC->W where C is camera coordinate system and W is world coordinate system. Any vector expressed in camera coordinate system multiplied by the below matrix would give us the same vector expressed in world coordinate system.
right.x up.x forward.x
camToWorld = right.y up.y forward.y
right.z up.z forward.z
The TW->C transformation would be
right.x up.x forward.x
worldToCam = inverse(right.y up.y forward.y)
right.z up.z forward.z
right.x right.y right.z
worldToCam = up.x up.y up.z
forward.x forward.y forward.z
Remember that the inverse of an orthogonal matrix is its transpose.
Allowing the camera to be placed anywhere
Since 3x3 matrices can’t encode translation we have to use 4x4 ones. We could just use 3x3 for the rotation/scale and vector addition for the translation but its easier to just use matrix multiplication for everything. Adding translation to the mix gives us the following transformation TC->W.
1 0 0 Tx right.x up.x forward.x 0
camToWorld = 0 1 0 Ty * right.y up.y forward.y 0
0 0 1 Tz right.z up.z forward.z 0
0 0 0 1 0 0 0 1
right.x up.x forward.x Tx
camToWorld = right.y up.y forward.y Ty
right.z up.z forward.z Tz
0 0 0 1
with TW->C being
right.x up.x forward.x 0 1 0 0 Tx
worldToCam = inverse(right.y up.y forward.y 0) * inverse(0 1 0 Ty)
right.z up.z forward.z 0 0 0 1 Tz
0 0 0 1 0 0 0 1
right.x right.y right.z 0 1 0 0 -Tx
worldToCam = up.x up.y up.z 0 * 0 1 0 -Ty
forward.x forward.y forward.z 0 0 0 1 -Tz
0 0 0 1 0 0 0 1
right.x right.y right.z -dot(T, right)
worldToCam = up.x up.y up.z -dot(T, up)
forward.x forward.y forward.z -dot(T, forward)
0 0 0 1
The only thing worth noting is that the translation is performed in different order based on the direction of transformation
- TC->W - translation is done after the change of basis transform
- TW->C - translation is done before the change of basis transform
In general, the inverse of a matrix product is the product of inverses in the opposite order (we are undoing the transformations from last applied to first applied).
(Translation * Change Of Basis) -1 = Change Of Basis -1 * Translation -1
What dictates when we should apply the translation in our case (camera <-> world) is the fact that the camera is itself in world coordinate system. Let’s look at an example as it will be easier to understand
Pworld = (1,3,2)
CamWorld = (5,2,1)
cam2world - transform from camera coordinate space to world coordinate space
world2cam - inverse(cam2world) ; transform from world space to camera space
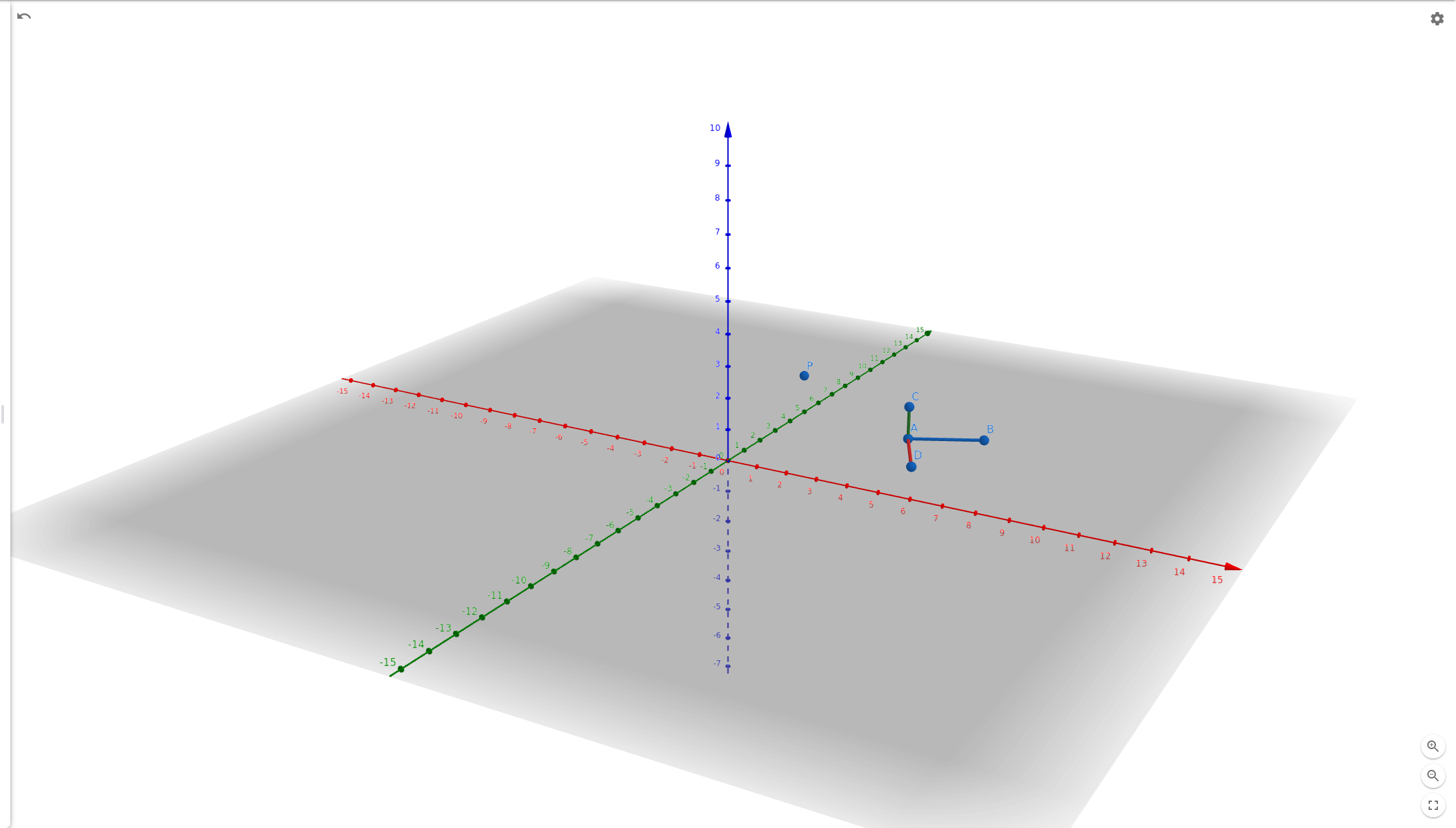
Task #1: Express the point in camera space
1. First we move the point to be relative to the camera
2. Next we apply the change of basis
relativePoint = Pworld - CamWorld
pointCamSpace = world2cam * relativePoint
Task #2: Express the pointCamSpace in world coordinate system
1. First we apply the inverse of the `world2cam` transform
2. Next we apply the translation to make the point relative to the world and not the camera
relativePoint = cam2world * pointCamSpace
Pworld = relativePoint + CamWorld
As you can see the above steps match the matrix multiplication order that we got previously.
This pretty much concludes the post on the camera transform, leave a comment below if you have any feedback or suggestions.